题解

我们的问题是计算长度为 k 的子序列的中位数总和，而其中的每个子序列都是一个二进制数组。由于二进制串中只有 0 和 1，所以子序列的中位数只可能是 0 或 1。且只有当中位数为 1 时，才会对答案产生贡献。因此，我们只需要关注中位数为 1 的子序列，忽略中位数为 0 的情况。

排序与有效子序列的构建

将数组 a 进行排序的原因在于，题目要求一个有效子序列的构建方式为 左边部分比右边部分小。排序后，我们可以方便地找到所有 1 并计算其左右部分的元素数量。

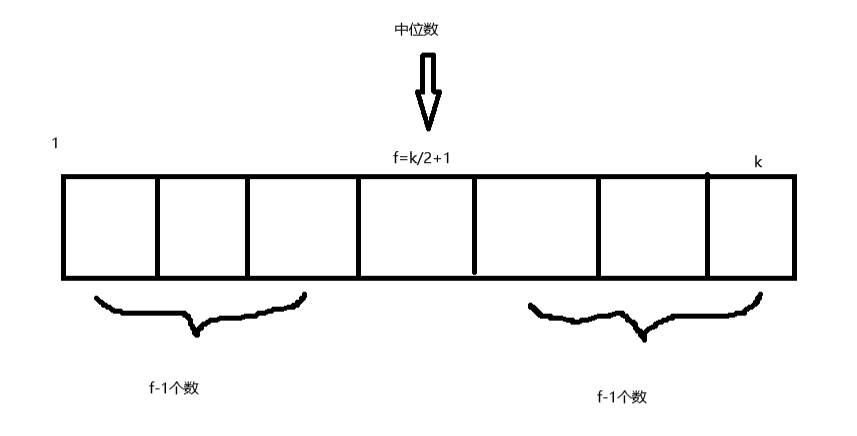
对于数组 a 中每个值为 1 的元素，假设它的位置是 i，则可以确定该元素的左侧和右侧分别有多少个元素：

int a = i - 1, b = n - i;

其中，a 表示左侧的元素数量，b 表示右侧的元素数量。

组合数的计算

当找到位置 i 上的 1 时，我们可以将它与左侧的 a 个元素中的 f - 1 个元素，以及右侧的 b 个元素中的 f - 1 个元素组合，构成一个有效的子序列（其中 f = k / 2 + 1 是中位数所在的位置）。

该 1 对答案的贡献为：

组合数的公式为：

代码示例

以下代码展示了如何计算每个位置为 1 的元素对答案的贡献：

for (int i = f; i <= n - f + 1; ++i)
{
    if (a[i] == 1)
    {
        int a = i - 1, b = n - i;
        ll num = get_c(a, f - 1) * get_c(b, f - 1) % mod;
        ans += num;
        ans %= mod;
    }
}

在该代码中：

• get_c(a, f - 1) 计算左侧 a 个元素中选取 f - 1 个的组合数。
• get_c(b, f - 1) 计算右侧 b 个元素中选取 f - 1 个的组合数。
• 每个 1 的贡献值累加到 ans 中，最终输出对答案的贡献总和。

代码

#include <bits/stdc++.h>
#define PI acos(-1)
#define all(a) (a).begin(), (a).end()
#define erjinzhi(n) __builtin_popcountll(n);
#define IOS                       \
    ios_base::sync_with_stdio(0); \
    cin.tie(0);                   \
    cout.tie(0);
// #pragma GCC optimize(2,"Ofast","inline")
using namespace std;
typedef long long ll;
typedef long double LD;
typedef pair<int, int> PII;
const char nl = '\n';
const int N = 2e5 + 10;
const int mod = 1e9 + 7;
int a[N], b[N];
int fact[N], infact[N]; // fact存阶乘 ，infact存阶乘的逆元

int qmi(int a, int n, int mod)
{ // 快速幂 求得 a^n % mod
    int res = 1;
    while (n)
    {
        if (n & 1)
            res = (ll)res * a % mod;
        a = (ll)a * a % mod;
        n >>= 1;
    }
    return res;
}
ll get_c(int a, int b)
{
    return (ll)fact[a] * infact[b] % mod * infact[a - b] % mod;
}
void solve()
{
    int n, k;
    cin >> n >> k;
    for (int i = 1; i <= n; ++i)
        cin >> a[i];
    sort(a + 1, a + 1 + n);
    int f = k / 2 + 1;
    ll ans = 0;
    for (int i = f; i <= n - f + 1; ++i)
    {
        if (a[i] == 1)
        {
            int a = i - 1, b = n - i;
            ll num = get_c(a, f - 1) * get_c(b, f - 1) % mod;
            ans += num;
            ans %= mod;
        }
    }
    cout << ans << nl;
}
int main()
{
    IOS;
    fact[0] = infact[0] = 1;
    for (int i = 1; i < N; i++)
    {
        fact[i] = (ll)fact[i - 1] * i % mod; // 预处理前5000的阶乘和逆元
        infact[i] = (ll)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
    }
    int t;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

题解.md